原帖由 ‧幻星〞 於 08-10-25 21:57 發表
滿足a^2+b^2=c^2的a,b,c稱為畢氏三元數
而他們的通式可寫成a=2xy,b=x^2-y^2,c=x^2+y^2 (x,y為正整數)
這只是一種構造的手法而已
看多了就會記起來=)
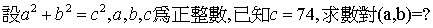
原帖由 ‧幻星〞 於 08-10-25 21:57 發表
滿足a^2+b^2=c^2的a,b,c稱為畢氏三元數
而他們的通式可寫成a=2xy,b=x^2-y^2,c=x^2+y^2 (x,y為正整數)
這只是一種構造的手法而已
看多了就會記起來=)

| 歡迎光臨 鐵之狂傲 (https://gamez.com.tw/) |