- 鐵幣
- 1885 元
- 文章
- 1396 篇
- 聲望
- 1332 枚
- 上次登入
- 15-11-14
- 精華
- 3
- 註冊時間
- 06-7-21
- UID
- 284795
|
1.Let R be a commutative ring with identity.
(a)Let I and J be ideals of R. Prove that I+J is the ideal generated by I∪J
(b)If I+J=R, prove that I∩J=IJ.
(c)Let R=Z24,I=<[4]> and J=<[6]>. Find I+J,I∩J, and IJ.
2.Let T={a/b |a/b belongs to Q, a and b are relatively prime and 5 does not divide b}
(a)Prove that T is a ring under usual addition and multiplication.
(b)Identify the unit group of T.
(c)Find a complete set of irreducible elements of T.
(d)Prove that I = {a/b |5 divides a} is an ideal of T and the quotient ring T/I is a field.
(e)Show that T is a PID.
3.Let F be a field and F[x,y] be the polynomial ring in variables x and y.
(a)Prove that the ideal <x> is a prime ideal but not maximal.
(b)Find a maximal ideal that contains the ideal <x>.
(c)Prove that F[x,y] is not a PID.
4.Answer the following true-or-false questions. If true, prove it; otherwise, disprove it.
(a)Every field is a PID.
(b)Let R be a commutative ring with identity. Then {0} is a maximal ideal if and only if R is a field.
(c)Let θ:Zp →R be a non-zero ring homomorphism where p is a prime. Then Zp is isomorphic some subring of R.
(d)A factor ring of an integral domain is still an integral domain.
(e)Any subgroup of the multiplicative group C* is cyclic.
5.Prove that in a commutative ring with identity, every nonzero prime ideal of finite index is maximal.
------------------------
Symbols Explanation:
Z=the set of all integers.
Q=the set of all rational numbers.
Zn=the set of remainders which is of a integer divided by n.(e.g.Z2={0,1})
1.
(a) List All irreducible polynomials of degree less than 4 over Z2.
(b) Show that f(x)=(x^4)+x+1 is irreducible over Z2.
(c) Contruct a finite field K of order 16 by using f(x) above. Let α=x+<f(x)> in K.
Express the general form of elements of K in terms of α.
(d) Realize the additive group <K,+>.(It means what group is isomorphic to <K,+>)
(e) Is K*=K-{0} cyclic under multiplication? If so, find a generator of K*.
(f) Find all the roots of f and show that K is a splitting field of f over Z2.
2. Test whether the following polynomials are irreducible over Q.
(a) f1(x)=(x^5)+9(x^4)+12(x^2)+6.
(b) f2(x)=8(x^3)-6x+1.
(c) f3(x)=(x^6)+(x^3)+1. (HINT: Use a suitable change of variable.)
(d) f4(x)=(3/7)(x^4)-(2/7)(x^2)+(9/35)(x)+3/5.
3.Show that 3(x^2)+4x+3 in Z5[x] factors as (3x+2)(x+4) and (4x+1)(2x+3).
Can you conclude that Z5[x] is not a UFD? Explain your answer.
4.
(a) Find the splitting field F of f(x)=(x^4)-2 over Q.
(b) Find the degree (F :Q).
(c) Find a basis ofF over Q.
(d) Write down two distinct subfields of degree 2 over Q between F and Q.
5. Answer the following true-or-false questions. If True, prove it;otherwise, disprove it.
(a) Z[x,y] is a UFD.
(b) 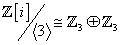 as rings. as rings.
(c) A simple algebraic extension must be a finite extention.
(d) If F is an infinite field, then the characteristic of F must be 0.
[ 本文最後由 傲月光希 於 07-6-16 10:18 PM 編輯 ] |
|






 發表於 07-4-9 23:11:12
發表於 07-4-9 23:11:12
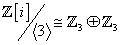 as rings.
as rings.